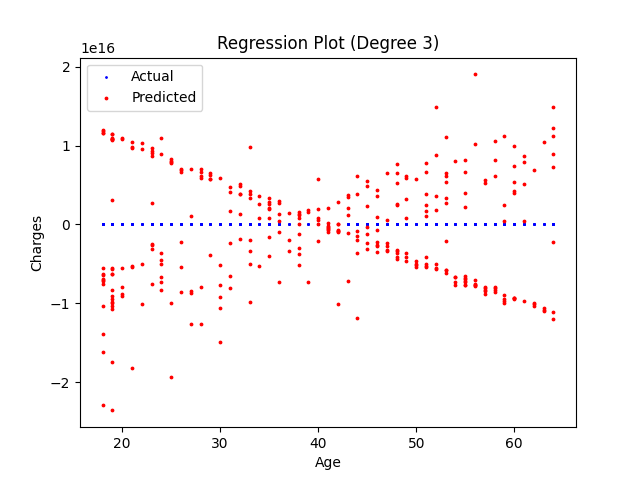
Regresja wielomianowa z wykorzystanem biblioteki Sklearn.
Analiza z wykorzytaniem regresji wielomianowej.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split
# Tworzymy dane syntetyczne: ceny (y) rosną nieliniowo względem wielkości (x)
np.random.seed(42)
X = np.linspace(0, 10, 100)
y = 2 + 3 * X - 0.5 * X ** 2 + np.random.normal(0, 2, size=X.shape) # nieliniowa zależność
X = X.reshape(-1, 1)
# Dzielimy dane na uczące i testowe
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
# Testujemy różne stopnie wielomianu
for degree in [1, 2, 3, 9]:
# Tworzymy cechy wielomianowe
poly = PolynomialFeatures(degree=degree)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)
# Trenujemy model
model = LinearRegression()
model.fit(X_train_poly, y_train)
# Predykcja
y_pred_train = model.predict(X_train_poly)
y_pred_test = model.predict(X_test_poly)
# Błędy
train_error = mean_absolute_error(y_train, y_pred_train)
test_error = mean_absolute_error(y_test, y_pred_test)
# Wydruk błędów
print(f"\nStopień wielomianu: {degree}")
print(f" Błąd MAE (train): {train_error:.2f}")
print(f" Błąd MAE (test): {test_error:.2f}")
# Wykres
plt.figure(figsize=(8, 4))
plt.scatter(X, y, color='blue', s=10, label='Dane rzeczywiste')
# Krzywa predykcji
X_range = np.linspace(0, 10, 300).reshape(-1, 1)
X_range_poly = poly.transform(X_range)
y_range_pred = model.predict(X_range_poly)
plt.plot(X_range, y_range_pred, color='red', linewidth=2, label=f'Dopasowanie (deg {degree})')
plt.title(f"Regresja wielomianowa (stopień {degree})")
plt.xlabel("X (np. wiek, rozmiar)")
plt.ylabel("Y (np. cena, koszty)")
plt.legend()
plt.grid(True)
plt.show()
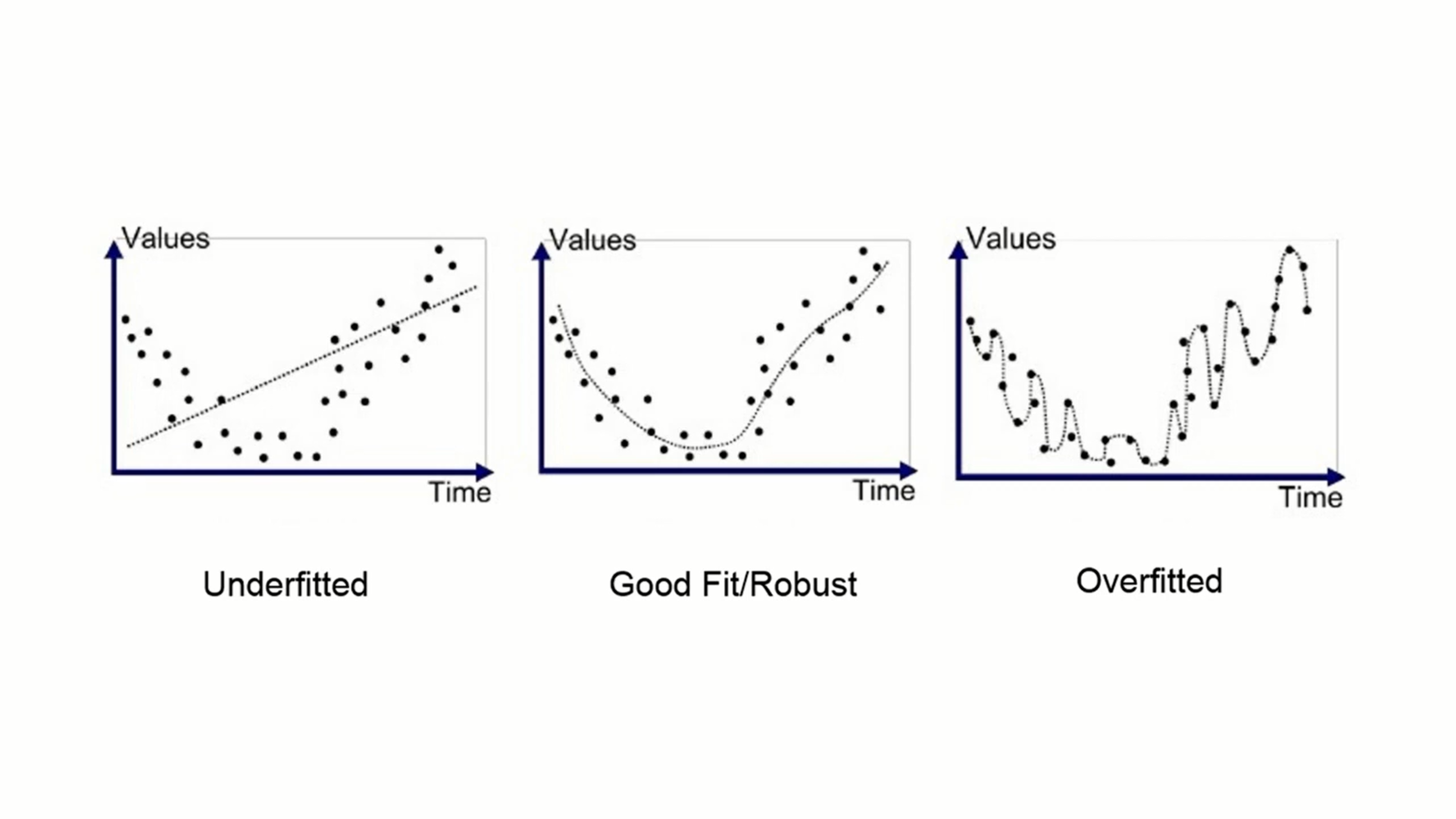
Wyjaśnienie zjawiska overfittingu. Jeżeli podążymy w wielomian zbyt wysokiego stopnia, mode będzie odwzorowywał dane uczące, ale słabo będzie przewidywał.
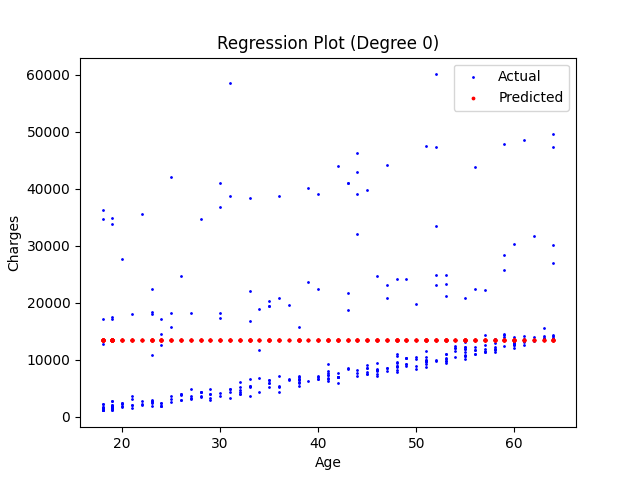
Wielomian 1 stopnia.
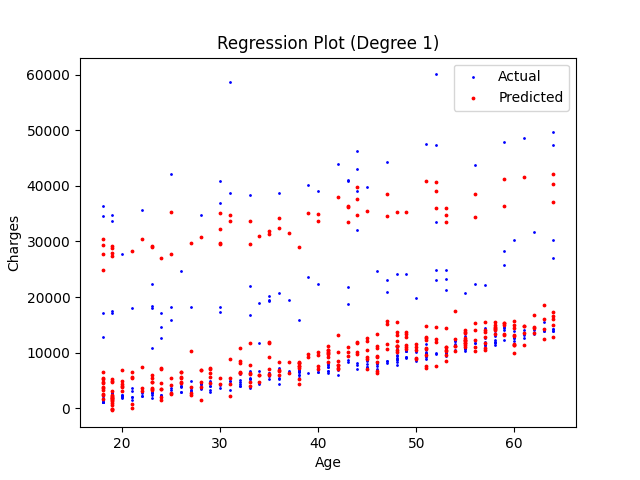
Wielomian 2 stopnia.
Wielomian 3 stopnia. Wartość "le13" w lewej górnej części wykresu oznacza potęgę do której podniesione są wartości osi y.
Wielomian 4 stopnia.